Data Quantization

In order to transfer large amounts of data between networks or even between CPU and GPU techniques called Data Quantization are employed. By analyzing the data and making careful approximations the data may be compressed into a smaller state.

In this case I will take a look at a networking scenario where I will reduce the required bandwidth of a networked-physics simulation.

Base Case

The initial state per object in the simulation is 64 Bytes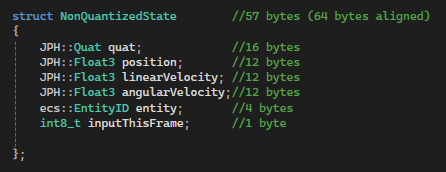

In order to simulate 1000 objects this would require a bandwidth of $(1000 * 64) = 64000$ bytes.
With a minimum frame-rate of 60 we would be sending this data 60 times per second resulting in $64000 * 60 = 3 840 000 $ bytes.
This is $3.8$ Mega-bytes per second.
Converting it to mega-bits per second gives us $3840000 * 8 / (1000 * 1000) = 30,72$ MBps per second.

This is a lot of data being sent per-frame.

Networked games have very different target bandwidths ranging from 1MBps - 50 MBps depending on the scale of the game. Most games lay between 1 and 10 MBps.

This is where compression techniques and other optimizations come into play.

Quantization Techniques

Zero-Point Quantization

Lets begin by analyzing the function that will be used to reduce a floating-point value to a smaller integer-range.

template<typename T,uint32_t bits>
inline T Quantize(float aVal, float aMin, float aMax)
{
	constexpr uint32_t nLevels = (1u << bits);
    constexpr uint32_t upperBound = nLevels - 1;
	float scale = (aMax - aMin) / upperBound; 
	int zeroPoint = static_cast<int>(std::round(-aMin / scale)); 
	float x = std::round(aVal / scale) + zeroPoint;
	T xQ = static_cast<T>(std::clamp(static_cast<int>(x), 0, static_cast<int>(upperBound)));

	return xQ;
}

Let’s run an example with the value being quantized as $42.78$ and we want to map it to a uint_8t
nLevels is the total number of discrete values in the quantized range, e.g $2^8 = 256$.
upperBound the upperbound to ensure overflow does not happen.
scale defines how much each integer step represents in he original floating point rage. e.g assuming aMin and aMax are $-128$ and $128$.
$scale = \frac{128 - (-128)} { (256 - 1)} ≈ 1.00392$
This will result in a fairly lossy quantization where the worst-case rounding approximately $0.50196$ pe

zeroPoint shifts the quantization in order to preserve the aMin value.
$zeroPoint = round(\frac{-(-128)} { 1.00392}) ≈ 128$

x becomes scaled and then shifted by the zeroPoint value to center it in the range.
$x = round(\frac {42.78} {1.00392}) + (128) ≈ 171$

xQ is our final quantized value, we clamp it to the max range and return it.
$xQ = 171$
Regarding how lossy the quantization becomes, it is important to reason about the data that is being quantized. There is no one solution fits all, one should reason about the data and find a range that fits the accepted precision level of the application.

template<typename T, uint32_t bits>
inline float Dequantize(T aVal, float aMin, float aMax)
{
    constexpr uint32_t nLevels = (1u << bits);
    constexpr uint32_t upperBound = nLevels - 1;
	float scale = (aMax - aMin) / (upperBound);
	int zeroPoint = static_cast<int>(std::round(-aMin / scale));
	float xF = (static_cast<int>(aVal) - zeroPoint) * scale;

	return xF;
}

Dequantization is achieved by rearranging our formula, while keeping it mostly the same.

$ xF = (171 - (128)) * 1.00392 ≈ 43.16856$

The data lost is equal to

$ 43.16856 - 42.78 = 0.38856 $

Finally it is only up to the user to verify if this is an acceptable loss of precision, if not one must reconsider the ranges the data may vary between.

Compressing the Quaternion

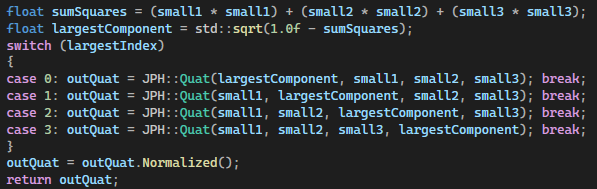
The largest component of the state we are sending is the Quaternion.
It stores the rotation of the object using four four byte values representing x,y,z,w.

A Quaternion storing a valid 3D rotation has a magnitude of 1 derived from $ \sqrt{x^2 + y^2 + z^2 + w^2} = 1 $.

By dropping one component it is possible to derive it from the largest three through substitution. Assuming $w$ is the largest component.

$w = \sqrt{1-x^2 + y^2 + z^2}$
Since the magnitude of the quaternion is calculated using the square root, $w$ may never be negative however a quaternion representing a 3D rotation may contain negative values, and since the method to compress a floating point value used an unsigned value this is a problem.

There is a property to a quaternion that will help.
$-x,-y,-z,-w$ in a quaternion represents the same rotation as $x,y,z,w$.
This means that if the component with the largest absolute value is negative, the entire quaternion may be negated and still contain a valid representation of the exact same rotation.

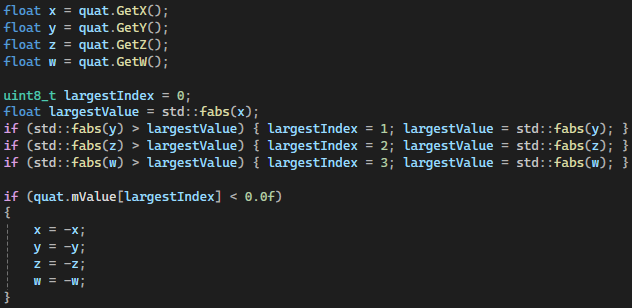
With the largest value found, it is now possible to extract the three smallest components and begin quantizing them.

With the goal of squishing all this data into a smaller format that we can serialize to a uint32_t which consists of 4 bytes or 32 bits, consider the amount of data needed per component.

The data that have to be stored is the index of the largest component (2 bits), that leaves 9 bits for each remaining component. 9 bits gives us $2^9 = 512$.
Therefor the integer range we can encode each component to is $[0,511]$.

Because the magnitude is 1 we can derive this from the fact that if the largest value a component can take is $v = 1$. The second largest is if two components have the same absolute value $\sqrt{v^2 + v^2} = \sqrt{2v^2} = \sqrt{2\frac{1}{2}} = \sqrt{1} = 1$.

This is proof of the min and max range for the quantization to achieve as much precision as possible. The range the quantization will encode into is $[-\sqrt{\frac{1}{2}},\sqrt{\frac{1}{2}} ]$

This is useful because it is now encoded in a larger precision since we are not encoding in $[-1,1]$.

In order to determine what the worst-case precision is we calculate it from the scale $maximumPrecisionLoss = \frac{scale}{2}$

Remembering from the quantization function the scale was calculated like this.

$scale = \frac{max - min}{upperBound} = \frac{\sqrt(\frac{1}{2}) -(-\sqrt(\frac{1}{2}))}{2^9 -1} = \frac{1.414}{511} = 0,0027 $
This gives a total worst-case precision loss of
$\frac{0,0027}{2} = 0,00138 $
All that is left of the Compression step now is to shift the values into a uint32_t by bitmasking and left shifting.

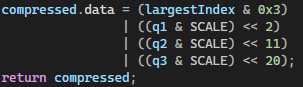
Decompression

On the recieving end we will now decompress the uint32_t compressed.data back into the original value with a slight precision loss.

Starting with shifting out the data and dequantizing it, the data is now in a state where we can begin to reconstruct the missing component.

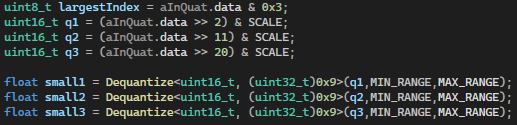
All that is left now is to take the combined sum of the largest components and reconstruct the quaternion, assuming $Y$ was the largest component leaves $Y = \sqrt{1 - X^2 + Z^2 + W^2}$.

Compressing Position and Velocity

Position and velocity is compressed by taking the difference from frame $A$ to frame $B$, compressing that value with zero-point compression and then creating a system on reciever side that says that frame $B$ is relative to frame $A$.

Maximum change must also be taken into account when considering the range that you may compress within.

If you need to do teleportation or larger positional changes, reconsider the approach taken or add the ability to send full uncompressed position occasionally.

Even with smaller positional changes clipping and other issues may start appearing, so a more sophisticated system that occasionally sends a full positional value may be required to adjust if the simulation have accumulated too much error.

Compression results

Original: 64 bytes -> Quantized 20 bytes final reduction of (68.75%).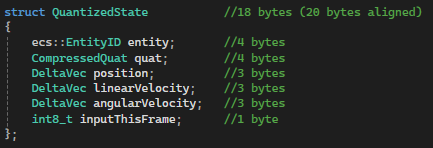

Other optimizations

The easiest one, do not send what is not needed.
If a cube has not moved in this frame do not send it.
On the recieving end just keep the object at the last known place.

Setting up client-server functionality

Messages, packets and buffers

To be able to send messages across networks I needed to be able to serialize and deserialize data. For that we need a base message class.

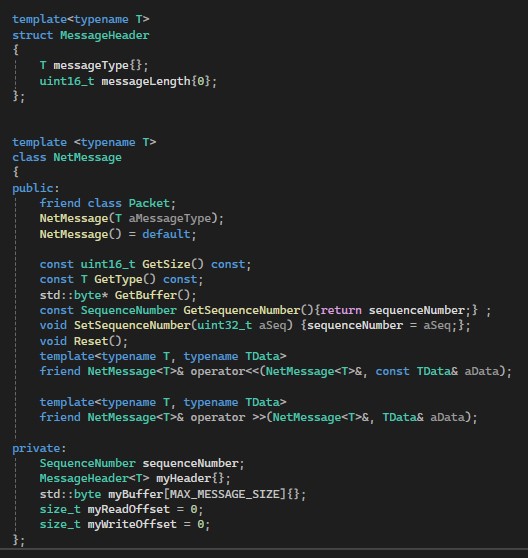
Each message consists of a message header that explicitly states what type the message is and the messageLength, the type here is a enum.
The message class overloads the out and in stream operators so we can write data and read data from the message.

We are going to be constructing multiple messages per update, and each frame we will send one state update so we need to be able to pack each individual message into a packet.

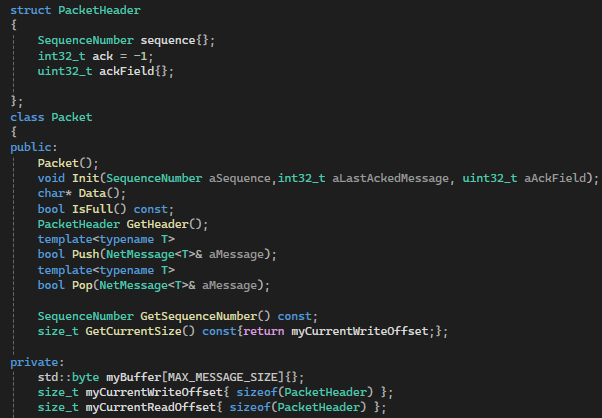
Each packet gets filled with as many messages as we can write each frame. The packet header tells us which sequence number the packet is part of.
Sequence number here doubles as the tick count.

The header also specifies a specific acked message and a ackfield. The ack is the most recent acked message, and the ackfield contains the most recent 32 acked messages.

This redundancy adds an extra layer of protection to acks gettings lost, for a relatively small price of 4 bytes.

When sending and recieving packages they get placed into sequence buffers The sequence buffer is a circular buffer giving us a fast and efficient way of storing data.

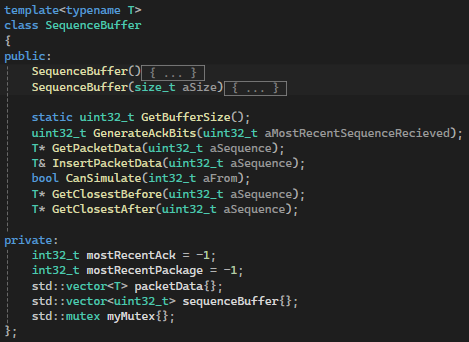
Each frame before sending a packet the sequence buffer constructs the package ackField by iterating over the N - 32 last packets and checking if they have been acked.

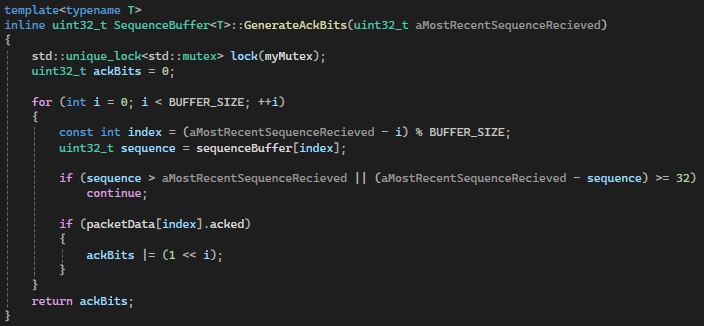
If the packets have not been acked when constructing packages before sending, the sender will resend that package if the roundtrip-time have been crossed as that package is assumed to have been lost.

Final Result